14. 总结
总结
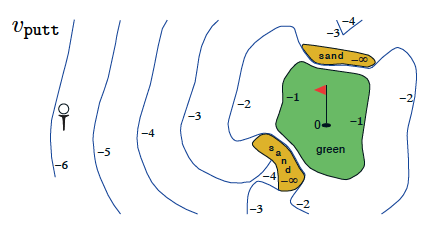
高尔夫智能体的状态值函数(Sutton 和 Barto,2017 年)
策略
确定性策略是从 \pi: \mathcal{S}\to\mathcal{A} 的映射。对于每个状态 s\in\mathcal{S},它都生成智能体在状态 s 时将选择的动作 a\in\mathcal{A}
随机性策略是从 \pi: \mathcal{S}\times\mathcal{A}\to [0,1]
的映射。对于每个状态 s\in\mathcal{S} 和动作 a\in\mathcal{A},它都生成智能体在状态 s 时选择动作 a 的概率。
状态值函数
- 策略 \pi 的状态值函数表示为 v_\pi。对于每个状态 s \in\mathcal{S},它都生成智能体从状态 s 开始,然后在所有时间步根据策略选择动作的预期回报。即 v_\pi(s) \doteq \text{} \mathbb{E}\pi[G_t|S_t=s]。我们将 v\pi(s) 称之为在策略 \pi 下的状态 s 的值。
- 记法 \mathbb{E}\pi[\cdot] 来自推荐的教科书,其中 \mathbb{E}\pi[\cdot] 定义为随机变量的预期值(假设智能体遵守策略 \pi)。
贝尔曼方程(第 1 部分)
- v_\pi 的贝尔曼预期方程是:v_\pi(s) = \text{} \mathbb{E}\pi[R{t+1} + \gamma v_\pi(S_{t+1})|S_t =s].
最优性
- 策略 \pi' 定义为优于或等同于策略 \pi(仅在所有 s\in\mathcal{S} 时 v_{\pi'}(s) \geq v_\pi(s))。
- 最优策略 \pi_ 对于所有策略 \pi 满足 \pi_ \geq \pi。最优策略肯定存在,但并不一定是唯一的。
- 所有最优策略都具有相同的状态值函数 v_*,称为最优状态值函数。
动作值函数
- 策略 \pi 的动作值函数表示为 q_\pi。对于每个状态 s \in\mathcal{S} 和动作 a \in\mathcal{A},它都生成智能体从状态 s 开始并采取动作 a,然后在所有未来时间步遵守策略时产生的预期回报。即 q_\pi(s,a) \doteq \mathbb{E}\pi[G_t|S_t=s, A_t=a]。我们将 q\pi(s,a) 称之为在状态 s 根据策略 \pi 采取动作 a 的值(或者称之为状态动作对 s, a 的值)。
- 所有最优策略具有相同的动作值函数 q_*,称之为最优动作值函数。
最优策略
- 智能体确定最优动作值函数 q_ 后,它可以通过设置 \pi_(s) = \arg\max_{a\in\mathcal{A}(s)} q_(s,a) 快速获得最优策略 \pi_。
贝尔曼方程(第 2 部分)
- q_\pi 的贝尔曼预期方程是:q_\pi(s,a) = \text{}\mathbb{E}\pi[R{t+1} + \gamma q_\pi(S_{t+1},A_{t+1})|S_t =s, A_t=a].
- v_ 的贝尔曼最优性方程是:v_(s) = \max_{a \in \mathcal{A}(s)} \mathbb{E}[R_{t+1} + \gamma v_*(S_{t+1}) | S_t=s]。
- q_ 的贝尔曼最优性方程是:q_(s,a) = \mathbb{E}[R_{t+1} + \gamma \max_{a'\in\mathcal{A}(S_{t+1})}q_*(S_{t+1},a') | S_t=s, A_t=a]。